3d Chapitre 2 - Transformations

CHAPITRE 2 - Transformations
Ce chapitre traite des différentes transformations possible sur un objet 3D, plus précisément les translations, les changements d’échelles et les rotations. Il est impératif que vous saisissiez bien les notions vues dans le chapitre 6 de la section 2D avant de poursuivre, car je n’expliquerai pas à nouveau la trigonométrie et les rotations 2D. Cependant, nous allons effectuer une révision rapide des notions mathématiques de base, bien qu’un cours complet d’algèbre linéaire est fortement conseillé.
ALGÈBRE LINÉAIRE
Révisons brièvement les notions de base de l’algèbre linéaire et de la géométrie analytique. Le vecteur en géométrie analytique est l’équivalent du nombre en algèbre. Un vecteur peut être imaginer comme une flèche qui pointe dans une certaine direction et possède une certaine longueur. Un vecteur peut être librement déplacé dans l’espace. Il est défini par ses composantes selon les trois axes x, y et z qui donnent sa longueur et sa direction.
Il existe plusieurs opérations réalisables sur les vecteurs. Pour faire la somme de deux vecteurs, on additionne leurs composantes respectives. La soustraction fonctionne de la même manière. La multiplication existe cependant sous 2 forme : le produit scalaire et le produit vectoriel. Soit a et b des vecteurs, produit vectoriel noté «.», et thêta : angle entre les vecteurs :
A . B = A B cos thêta
A . B =
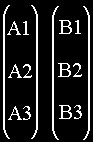
A1*B1 + A2*B2 + A3*B3
En isolant cos dans l’équation du produit vectoriel, on peut obtenir l’angle entre deux vecteur. En fait, on obtient le cosinus de cet angle. Soulignons cependant que très souvent, c’est précisément ce que l’on recherche. Si on désire l’angle, on utilisera alors arccos. Le produit vectoriel quant à lui associe à deux vecteurs un troisième qui est perpendiculaire (orthogonale) aux deux premiers. En voici la définition exacte :
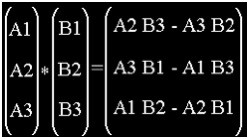
Les opérations sur les vecteurs sont utiles quand il s’agit de déterminer si une face est cachée et dans les calculs d’ombrages.
MATRICES DE TRANSFORMATIONS
Si on veut animer nos objets 3D sur l’écran, il va falloir leur faire subir des translations, des rotations et des changements d’échelle. Les transformations géométriques peuvent être représentée très élégamment dans des matrices. Une matrice est tout simplement un tableau à 2 dimensions de nombres réels. Nous utilisons ces matrices pour transformer nos coordonnées locales en coordonnées du monde 3D. Chacune de ces opérations transforme un vecteur par l’entremise d’une multiplication vecteur-matrice. Ces matrices sont généralement représentées sous la forme 3x3. Cependant, il est possible de combiner plusieurs matrices ensemble afin de pouvoir travailler avec une seule matrice. On appelle cette dernière la matrice de transformation homogène. Nous verrons comment construire cette matrice un peu plus loin.
MATRICE DE CHANGEMENTS D’ÉCHELLE
Le changement d’échelle permet à un objet de changer de taille, donc de l’agrandir ou de le rapetisser. Une telle transformation s’exprime par la matrice suivante :
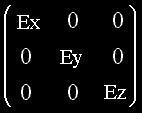
Pour changer l’échelle d’un objet par un facteur de 3, nous devons inscrire dans ex, ey et ez la valeur 3 et multiplier les vecteurs formant cet objet par la matrice en question. Ceci revient au même de multiplier chaque composante d’un vecteur par 3. Bien que cette dernière méthode semble plus rapide, n’oublions pas que nous cherchons par la suite à construire une matrice homogène. Nous avons donc besoin de la représentation matricielle.
MATRICES DE ROTATION
Les rotations 3D ne sont en fait qu’un série de rotation 2D. Pour passer en 3D, il suffit d'ajouter une dimension à notre matrice. Le hic, c’est qu’il ne faut pas que nos transformations sur un axe modifie les composantes X des coordonnées locales de l’objet. Chaque axe requiert donc une matrice unique. Il faut s’assurer que la rotation autour de l'axe des X ne modifiera pas les composantes X des coordonnées des coordonnées locales de l’objet, ainsi de suite pour les autres axes :
Matrice X
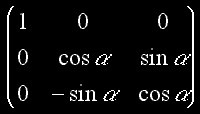
Matrice Y
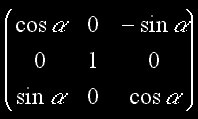
Matrice Z
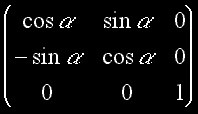
Finalement, nous voulons construire une matrice de translation. Cependant, nous ne pouvons pas effectuer une translation sur un vecteur en utilisant des combinaisons linéaires. Multiplier un vecteur par une matrice de translation produirait en effet un nouveau vecteur. Si on peut exprimer une translation par l’entremise d’une combinaison linéaire, nous pouvons maintenant construire une matrice de translation. Une solution populaire est d’utiliser le système de coordonnées homogènes. Dans ce nouveau système, chaque vecteur à 4 composante, x,y,z et la coordonnée homogène w, initialement à 1. Nous pouvons à présent effectuer une translation en utilisant des combinaisons linéaires :
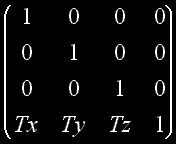
Cette nouvelle matrice vient cependant brouiller les cartes. En effet, nos anciennes matrices ne fonctionnent plus, car le produit d’un matrice de 4x4 par une matrice de 3x3 est indéterminé. Fort heureusement, nos anciennes matrices se transforme tout aussi facilement en matrice de 4x4 :
Matrice homogène de changement d’échelle

Matrice homogène de rotation X
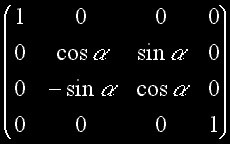
Matrice homogène de rotation Y
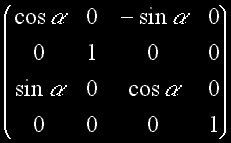
Matrice homogène de rotation Z

PROGRAMMATION GRAPHIQUE 3D
Après cette attaque massive de mathématique, nous allons maintenant regarder l’aspect plus pratique de ce chapitre, la programmation. Il nous faudra tout d’abord des structures de donnée pour représenter nos objets. Tout d’abord, étant donné le nombre considérable de variables matricielles, il serait très utile d’avoir un type définissant une matrice de 4x4 de nombre réels :
typedef float _mat4x4[4][4]; // type matrice reelle de 4x4
Ensuite, un type pour nos coordonnées 2D et 3D simplifierait beaucoup les choses :
typedef struct _2D // Structure pour representer un point dans un espace 2D
{
int x,y;
};
typedef struct _3D // Structure pour representer un point dans un espace 3D
{
float x,y,z;
};
Nous allons avoir besoin d’un type pour représenter les sommets de nos objets. Comme nous avons dans le chapitre 1, ces sommets s’expriment différemment selon la référence qu’on utilise (Écran, Caméra, Monde et Local). Nous allons donc avoir besoin de ces différents types de données dans notre type sommet. Finalement, notre type objet composé pour l’instant d’un nombre de sommet et d’un tableau de sommets:
typedef struct _sommet // Structure pour represente un sommet
{
_3D local; // coordonnees locales
_3D monde; // coordonnees dans le monde
_2D ecran; // coordonnees d'ecran
};
typedef struct _objet // Structure pour contenir un objet
{
int nbsommet; // nombre de sommets
_sommet sommet[12]; // coordonnees des sommets
};
Nous pouvons donc à présent définir un objet, avec un ensemble de sommets le représentant. Avec cette représentation très simple, nous pouvons écrire un petit programme qui affichera les sommets (sous forme de pixel) et qui les animera selon les transformations que nous ferons subir à notre objet. Voyons en détail le code de ces transformations. Pour chaque matrices, nous allons devoir l’initialiser en tant que matrice identité, c’est à dire une matrice vierge avec l’élément 1 en diagonale à (0,0), (1,1) et (2,2). Naturellement, comme nous travaillons avec une matrice homogène, il ne faut pas oublier w à (3,3). Cette fonction crée une matrice identité :
void ident_matrice(_mat4x4 m)
{
memset(m,NULL,sizeof(_mat4x4)); // 1 0 0 0
m[0][0] = 1.0; // 0 1 0 0
m[1][1] = 1.0; // 0 0 1 0
m[2][2] = 1.0; // 0 0 0 1
m[3][3] = 1.0; // matrice identité
}
Nous allons maintenant devoir effectuer 2 opérations pour construire notre matrice homogène. Premièrement, la multiplication matricielle, qui multiplie chaque éléments d’une matrice 4x4 par une autre, et deuxièmement une fonction pour copier nos matrices temporaires dans la matrice globale.
void copie_matrice(_mat4x4 source, _mat4x4 dest)
{
memcpy(dest,source,sizeof(_mat4x4));
}
void mult_matrice(_mat4x4 m1, _mat4x4 m2, _mat4x4 dest)
{
for(short i=0;i<4;i++)
for(short j=0;j<4;j++)
dest[i][j] = m1[i][0]*m2[0][j]+
m1[i][1]*m2[1][j]+
m1[i][2]*m2[2][j]+
m1[i][3]*m2[3][j];
} Nos matrices de rotations, changement d’échelle et translation sont crées à partir des matrices que nous avons vu plus haut. Le principe est le même pour chaque matrice : on initialise la matrice (matrice identité), on insère les paramètres dans la matrice et on multiplie la matrice correspondante par la matrice globale homogène, plaçant le résultat dans une matrice temporaire. Le résultat final est ensuite copié dans la matrice globale homogène.
void echelle(_mat4x4 m,float ex,float ey, float ez)
{
_mat4x4 emat; // matrice échelle
ident_matrice(emat); // initialise matrice identité
emat[0][0]=ex; // ex 0 0 0
emat[1][1]=ey; // 0 ey 0 0
emat[2][2]=ez; // 0 0 ez 0
// 0 0 0 1
mult_matrice(m,emat,m1); // (emat X m) -> m1
copie_matrice(m1,m); // copie le résultat dans matrice
} // globale de transformation homogène
void translation(_mat4x4 m,float tx,float ty,float tz)
{
_mat4x4 tmat; // matrice translation
ident_matrice(tmat); // initialise matrice identité
tmat[3][0]=tx; // 1 0 0 0
tmat[3][1]=ty; // 0 1 0 0
tmat[3][2]=tz; // 0 0 1 0
// tx ty tz 1
mult_matrice(m,tmat,m1); // (tmat X m) -> m1
copie_matrice(m1,m); // copie le résultat dans matrice
} // globale de transformation homogène
void rotation(_mat4x4 m,int ax,int ay,int az)
{
_mat4x4 xmat, ymat, zmat;
ident_matrice(xmat);
ident_matrice(ymat);
ident_matrice(zmat);
xmat[1][1] = COS(ax); xmat[1][2] = SIN(ax);
xmat[2][1] = -SIN(ax); xmat[2][2] = COS(ax);
ymat[0][0] = COS(ay); ymat[0][2] = -SIN(ay);
ymat[2][0] = SIN(ay); ymat[2][2] = COS(ay);
zmat[0][0] = COS(az); zmat[0][1] = SIN(az);
zmat[1][0] = -SIN(az); zmat[1][1] = COS(az);
mult_matrice(m,ymat,m1);
mult_matrice(m1,xmat,m2);
mult_matrice(m2,zmat,m);
}
L’ordre dans lequel on effectue nos transformations importe peu. Une fois la matrice construite, nous obtenons une matrice qui pourrait se résumer ainsi :
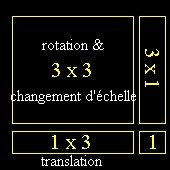
Une fois notre matrice homogène construite, nous sommes enfin prêt à transformer nos coordonnées locale en coordonnées du monde. Il faudra maintenant une fonction pour multiplier chaque vecteur (sommet) de l’objet par la matrice. Finalement, chaque sommet verra ses coordonnées de monde transformée en coordonnées d’écran par l’équation de projection :
void projection(_sommet *sommet)
{
sommet->ecran.x = sommet->monde.x * DISTANCE / sommet->monde.z + MX;
sommet->ecran.y = sommet->monde.y * DISTANCE / sommet->monde.z + MY;
}
void transformation(_objet *object, _mat4x4 m)
{
int v;
_sommet *sommet;
for(v=0; v<object->nbsommet; v++)
{
sommet = &object->sommet[v];
sommet->monde.x = sommet->local.x*m[0][0]+
sommet->local.y*m[1][0]+
sommet->local.z*m[2][0]+
m[3][0];
sommet->monde.y = sommet->local.x*m[0][1]+
sommet->local.y*m[1][1]+
sommet->local.z*m[2][1]+
m[3][1];
sommet->monde.z = sommet->local.x*m[0][2]+
sommet->local.y*m[1][2]+
sommet->local.z*m[2][2]+
m[3][2];
projection(sommet);
}
}
Pour les premiers exemples, nous allons utiliser une figure géométrique très simple, le cube. Après avoir initialiser correctement ses sommet, nous allons lui faire subir l’ensemble des transformations requises afin de pouvoir afficher ses sommets, sous forme de pixels, à l’écran. Voici la boucle principale :
ident_matrice(matrice);
echelle(matrice,20,20,20);
rotation(matrice,angle,angle,angle);
translation(matrice,0,0,-100);
transformation(&cube,matrice);
La fonction qui dessinera les sommets ne fera que qu’afficher un pixel pour chaque sommet, à l’aide de ses coordonnées d’écran. Remarquer l'utilisation de tables pré-calculé de sinus/cosinus. En effet, il serait ridicule de calculer tous ces angles en temps réel. La macro SIN et COS permette d'adresser la bonne valeur dans le tableau sinus/cosinus.
En résumé :
- Utiliser une matrice homogène pour simplifier les transformations géométriques
- Opérations sur les vecteurs (produit scalaire et vectoriel)
- Opérations sur les matrices
- Modélisation des sommets à partir des coordonnées d’écran
3dchap2.cpp
//////////////////////////////////////////////////////////////////////////
// Code source : Shaun Dore //
// Fichier : 3DCHAP2B.CPP //
// Date : 29-10-1998 //
// Compilateur : Borland C++ 3.1 //
// Description : Rotation 3D //
//////////////////////////////////////////////////////////////////////////
// --------------------------- INCLUDE --------------------------------//
#include <mem.h>
#include <math.h>
#include <conio.h>
// ---------------------- CONSTANTES & MACROS --------------------------//
#define MX 160 // Millieu de l'abscisse
#define MY 100 // Millieu de l'ordonnee
#define DISTANCE 200 // Distances de l'objet
#define SIN(x) SinTable[x] // Macro SIN()
#define COS(x) CosTable[x] // Macro COS()
// ------------------- STRUCTURES DE DONNEES --------------------------//
// type matrice reelle de 4x4
typedef float _mat4x4[4][4];
// Structure pour representer un point dans un espace 2D
typedef struct _2D
{
int x,y;
};
// Structure pour representer un point dans un espace 3D
typedef struct _3D
{
float x,y,z;
};
// Structure pour represente un sommet
typedef struct _sommet
{
_3D local; // coordonnees locales
_3D monde; // coordonnees dans le monde
_2D ecran; // coordonnees d'ecran
};
// Structure pour contenir un objet
typedef struct _objet
{
int nbsommet; // nombre de sommets
_sommet sommet[12]; // coordonnees des sommets
};
//------------------------- VARIABLES GLOBALES --------------------------//
// Utilise pour initialiser les coordonnes locales d'un objet de type cube
_3D Cube[8] = {
{ 1.0, 1.0, 1.0 },
{ -1.0, 1.0, 1.0 },
{ -1.0, -1.0, 1.0 },
{ 1.0, -1.0, 1.0 },
{ 1.0, 1.0, -1.0 },
{ -1.0, 1.0, -1.0 },
{ -1.0, -1.0, -1.0 },
{ 1.0, -1.0, -1.0 }
};
char *ecran = (char *) (0xA0000000L); // Memoire video
char *virtuel = new char[64000L]; // Ecran virtuel
float SinTable[360]; // Table Sinus
float CosTable[360]; // Table Cosinus
_mat4x4 matrice; // mat de transformation homogene
_mat4x4 m1, m2; // matrices temporaires
// ------------------------- FONCTIONS --------------------------------//
/////////////////////////////////////////////////////////////////////////
// putpixel - affiche un pixel sur l'ecran virtuel //
/////////////////////////////////////////////////////////////////////////
void putpixel (int x, int y, unsigned char col)
{
virtuel[(y<<8)+(y<<6)+x] = col;
}
/////////////////////////////////////////////////////////////////////////
// precalc - Calcule le tableau de sinus/cosinus //
/////////////////////////////////////////////////////////////////////////
void precalc()
{
for(int angle=0; angle<360; angle++)
{
SinTable[angle]=sin(angle*M_PI/180.0);
CosTable[angle]=cos(angle*M_PI/180.0);
}
}
/////////////////////////////////////////////////////////////////////////
// copie_matrice - copie une matrice source vers matrice destination //
/////////////////////////////////////////////////////////////////////////
void copie_matrice(_mat4x4 source, _mat4x4 dest)
{
memcpy(dest,source,sizeof(_mat4x4));
}
/////////////////////////////////////////////////////////////////////////
// mult_matrice - multiplie 2 matrices et mets le resultat dans dest //
/////////////////////////////////////////////////////////////////////////
void mult_matrice(_mat4x4 m1, _mat4x4 m2, _mat4x4 dest)
{
for(short i=0;i<4;i++)
for(short j=0;j<4;j++)
dest[i][j] = m1[i][0]*m2[0][j]+
m1[i][1]*m2[1][j]+
m1[i][2]*m2[2][j]+
m1[i][3]*m2[3][j];
}
/////////////////////////////////////////////////////////////////////////
// ident_matrice - construit une matrice identite //
/////////////////////////////////////////////////////////////////////////
void ident_matrice(_mat4x4 m)
{
memset(m,NULL,sizeof(_mat4x4)); // 1 0 0 0
m[0][0] = 1.0; // 0 1 0 0
m[1][1] = 1.0; // 0 0 1 0
m[2][2] = 1.0; // 0 0 0 1
m[3][3] = 1.0; // matrice identite
}
/////////////////////////////////////////////////////////////////////////
// echelle - matrice de changement d'echelle //
/////////////////////////////////////////////////////////////////////////
void echelle(_mat4x4 m,float ex,float ey, float ez)
{
_mat4x4 emat; // matrice echelle
ident_matrice(emat); // initialise matrice identite
emat[0][0]=ex; // ex 0 0 0
emat[1][1]=ey; // 0 ey 0 0
emat[2][2]=ez; // 0 0 ez 0
// 0 0 0 1
mult_matrice(m,emat,m1); // (emat X m) -> m1
copie_matrice(m1,m); // copie le resultat dans matrice
} // globale de transformation homogene
/////////////////////////////////////////////////////////////////////////
// translation - matrice de translation //
/////////////////////////////////////////////////////////////////////////
void translation(_mat4x4 m,float tx,float ty,float tz)
{
_mat4x4 tmat; // matrice translation
ident_matrice(tmat); // initialise matrice identite
tmat[3][0]=tx; // 1 0 0 0
tmat[3][1]=ty; // 0 1 0 0
tmat[3][2]=tz; // 0 0 1 0
// tx ty tz 1
mult_matrice(m,tmat,m1); // (tmat X m) -> m1
copie_matrice(m1,m); // copie le resultat dans matrice
} // globale de transformation homogene
/////////////////////////////////////////////////////////////////////////
// rotation - matrices de rotations //
/////////////////////////////////////////////////////////////////////////
void rotation(_mat4x4 m,int ax,int ay,int az)
{
_mat4x4 xmat, ymat, zmat;
ident_matrice(xmat);
ident_matrice(ymat);
ident_matrice(zmat);
xmat[1][1] = COS(ax); xmat[1][2] = SIN(ax);
xmat[2][1] = -SIN(ax); xmat[2][2] = COS(ax);
ymat[0][0] = COS(ay); ymat[0][2] = -SIN(ay);
ymat[2][0] = SIN(ay); ymat[2][2] = COS(ay);
zmat[0][0] = COS(az); zmat[0][1] = SIN(az);
zmat[1][0] = -SIN(az); zmat[1][1] = COS(az);
mult_matrice(m,ymat,m1);
mult_matrice(m1,xmat,m2);
mult_matrice(m2,zmat,m);
}
/////////////////////////////////////////////////////////////////////////
// projection - transformation 3D -> 2D //
/////////////////////////////////////////////////////////////////////////
void projection(_sommet *sommet)
{
sommet->ecran.x = sommet->monde.x * DISTANCE / sommet->monde.z + MX;
sommet->ecran.y = sommet->monde.y * DISTANCE / sommet->monde.z + MY;
}
/////////////////////////////////////////////////////////////////////////
// transformation - multiplication de chaque sommet par la matrice //
/////////////////////////////////////////////////////////////////////////
void transformation(_objet *object, _mat4x4 m)
{
int v;
_sommet *sommet;
for(v=0; v<object->nbsommet; v++)
{
sommet = &object->sommet[v];
sommet->monde.x = sommet->local.x*m[0][0]+
sommet->local.y*m[1][0]+
sommet->local.z*m[2][0]+
m[3][0];
sommet->monde.y = sommet->local.x*m[0][1]+
sommet->local.y*m[1][1]+
sommet->local.z*m[2][1]+
m[3][1];
sommet->monde.z = sommet->local.x*m[0][2]+
sommet->local.y*m[1][2]+
sommet->local.z*m[2][2]+
m[3][2];
projection(sommet);
}
}
/////////////////////////////////////////////////////////////////////////
// Initialisation des sommets de l'objet //
/////////////////////////////////////////////////////////////////////////
void initialise_objet(_objet *objet)
{
objet->nbsommet=8;
for (int i=0;i<objet->nbsommet;i++)
{
objet->sommet[i].local.x=Cube[i].x;
objet->sommet[i].local.y=Cube[i].y;
objet->sommet[i].local.z=Cube[i].z;
}
}
/////////////////////////////////////////////////////////////////////////
// dessine_objet - dessine les sommets de l'objet //
/////////////////////////////////////////////////////////////////////////
void dessine_objet(_objet *objet)
{
for(int i=0;i<objet->nbsommet;i++)
putpixel(objet->sommet[i].ecran.x, objet->sommet[i].ecran.y, 31);
}
//------------------------ FONCTION PRINCIPALE -------------------------//
void main(void)
{
int angle=0;
_objet cube;
asm {MOV AX,0x13; INT 0x10}
precalc();
initialise_objet(&cube);
while(!kbhit())
{
memset(virtuel,0,64000L);
ident_matrice(matrice);
echelle(matrice,20,20,20);
rotation(matrice,angle,angle,angle);
translation(matrice,0,0,-100);
transformation(&cube,matrice);
dessine_objet(&cube);
while(!(inp(0x3DA)&8));
memcpy(ecran,virtuel,64000L);
if (angle++ == 359) angle = 0;
};
delete []virtuel;
asm {MOV AX,0x03; INT 0x10}
}